Algebra
Algebra er læran um roknihættirnar og um sambandið ímillum tøl. Í algebra verða bókstavir ofta settir í staðin fyri tøl. Hetta er fyri at leggja dent á, at teir roknihættir, vit brúka, galda ikki bara fyri einstøk tøl. Algebra verður tí eisini nevnd bókstavarokning. Algebra stavar frá 9. øld, tá ið støddfrøðingurin Al Khwarizmi gav eina bók í støddfrøði út í Bagdad. Hann nevndi bókina Al-jabr wa’l-muqabala. Tað man vera hetta Al-jabr, sum er blivið til algebra. Í algebra rokna vit við tølum, sum vit ikki vita, hvørji eru enn. Orsøkin til, at vit kunnu gera tað, er, at nógvar útrokningar eru eins, hvørji tøl vit so brúka. Algebraframsagnir eru nøvn á tølum, sum eru sett saman av bókstavum og tølum. Ofta kunnu tær skrivast styttri. Vit siga tá, at tað ber til at umstytta algebraframsagnirnar. Líka til 1637 var støddfrøðin týðiliga býtt sundir í algebra og geometri. Tá gav franska flogvitið í støddfrøði René Descartes út bók sína Discours de la méthode. Í einum ískoyti vísti hann á styrkina at tvinna algebraina og geometriina saman. Hetta gjørdist seinni til sjálvstøðugu vísindagreinina analýtisk geometri. Bókstavarokning verður serliga nýtt í kjarnaøkjunum geometri og funksjónir.
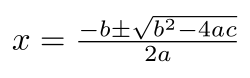
Er í einari líkning, verður hon nevnd líkning á øðrum stigi. Eina skipaða og umstytta líkning á øðrum stigi skriva vit:
Roknireglur
rætta- Fortekn
- Umstytting
- kann verða umstytt til
- Potensar
- givið at
- Undirskilt falditekn
- Tá ið vit skriva , er tað undirskilt, at tað merkir . Framsøgnina skriva vit vanliga
- Undirskilt pluss
- Tá ið einki fortekn stendur frammanfyri einum klombri ella tali, er tað undirskilt, at tað er pluss. T.d.:
- Undirskilt 1 tall
- Stendur eitt minustekn frammanfyri einum klombri, er tað undirskilt, at har stendur eitt 1 tal:

